一百多年前，爱因斯坦的相对论横空出世，彻底颠覆了人们传统的时空观。

在这之前，牛顿的绝对时空观深入人心，它非常符合我们的日常认知，让我们理所当然地认为时间和空间是绝对且一成不变的。

相对论主要包含狭义相对论和广义相对论，狭义相对论是广义相对论的基础，而广义相对论则是狭义相对论的推广，其具有更广泛的普适性。相对论中有一个极为重要的思想 —— 时间膨胀效应，也被称为钟慢效应。

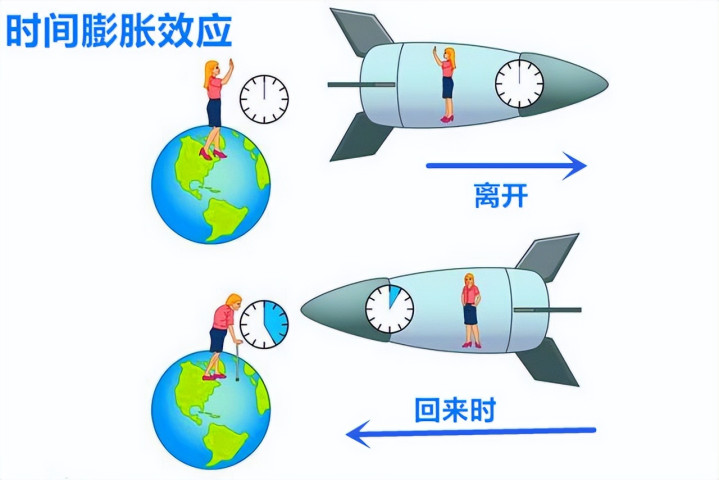
这一效应揭示了速度和引力都会对时间流逝的速度产生影响 。简单来说，就是速度越快，引力越强，时间流逝的速度就会越慢。从更深层次去理解，时间膨胀效应实际上体现了时间、空间和物质三者之间的紧密关系。

时间和空间并非彼此孤立，而是不可分割的整体，我们将其简称为 “时空”。

在这个宇宙中，你永远不可能找到没有时间的空间，反之，也不存在没有空间的时间。同时，物质的运动也会对周围的时空造成影响。

著名科幻电影《星际穿越》中就有一个令人印象深刻的情节，完美地展现了时间膨胀效应。主人公库珀一行人在执行任务时，来到了一颗靠近黑洞的星球 —— 米勒星球。

在这个星球上，时间发生了极为奇特的变化，仅仅停留一个小时，地球上的时间竟然已经过去了七年之久，时间膨胀倍数高达六万倍！

这个情节让无数观众惊叹不已，同时也引发了大家对于时间膨胀效应的强烈好奇：这种神奇的现象究竟是如何产生的呢？人类是否真的能够利用时间膨胀实现永生的梦想呢？

根据相对论，时间膨胀效应主要由速度和引力这两个因素引起 。

在狭义相对论中，速度对时间的影响遵循这样的规律：速度越快，时间流逝速度就越慢 。这一效应可以用时间膨胀公式来精确描述：t'=t/√[1-(v/c)²]。

在这个公式里，t'表示运动物体所经历的时间，也就是变慢后的时间（高速飞行的时间流逝）；t代表观测者的时间（低速世界）；v是运动物体相对低速世界的速度；c\则是光速，其数值约为每秒 299792458 米 。

从这个公式中我们可以清晰地看出，当物体的运动速度逐渐增大并接近光速时，分母的值会越来越小，从而使得t'的值逐渐增大，即时间流逝速度变慢 。

根据公式计算，物体运动一年，地球时间则过去了约 7.0888 年，时间膨胀效应变得非常明显，膨胀倍数达到了 7 倍左右 。由此可见，只有当物体的速度非常接近光速时，时间膨胀效应才会显著地体现出来 。

在广义相对论中，引力对时间的影响机制则是：引力越强，时间流逝速度越慢 。这一效应同样可以用相应的公式来表达：t'=tx√(1-2GM/rc²) 。

其中，t'为引力时间膨胀效应值；t为低引力惯性系观测者时间流逝值；G是万有引力常数；\(M\) 表示天体质量；r为物体到天体中心的距离；c依然是光速 。

例如，在地球表面，由于地球的质量和半径相对固定，引力相对较弱，时间膨胀效应并不明显 。

然而，在黑洞附近，情况则截然不同 。黑洞是一种质量极其巨大、引力极其强大的天体，其引力场强度远远超出了我们的想象 。

当物体靠近黑洞时，r值变得极小，而M值又极大，导致公式中分母的值迅速增大 。如果在低引力惯性系观测者的时间t过去了七年，那么在黑洞附近的时间t'则仅仅过去了七年的六万分之一，大约相当于一个小时 。

这也就解释了为什么在《星际穿越》中，主人公在黑洞附近停留了一个小时，而地球上的时间却过去了七年之久，时间膨胀倍数高达六万倍 。

黑洞最为显著的特征之一，便是其超强的引力 。

这种引力之强，超乎了我们的想象 。根据广义相对论，质量和能量会使时空发生弯曲，而黑洞由于其极高的密度和质量，产生的引力场极其强大，进而对周围的时空结构造成严重的扭曲 。可以想象，时空就像是一张巨大而平坦的弹性薄膜，而黑洞就如同一个质量极大的铅球放置在这张薄膜上 。铅球的重量会使薄膜发生凹陷，形成一个深深的 “引力井” 。

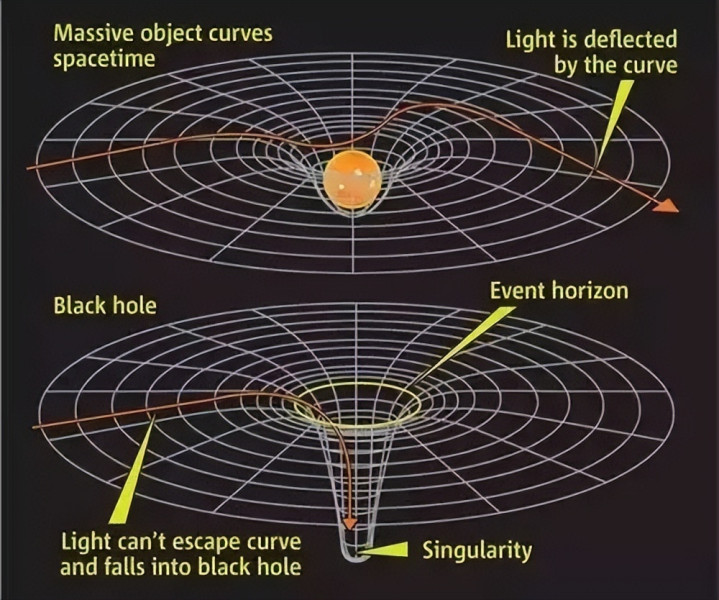
在黑洞周围，时空的弯曲程度极大，就好像这个 “引力井” 变得极为陡峭和深邃 。任何物体一旦进入黑洞的一定范围内，就会被其强大的引力所捕获，如同掉进了一个无法逃脱的深渊 。即使是光，这个宇宙中速度最快的存在，一旦进入黑洞的事件视界，也无法逃脱被吞噬的命运 。

事件视界是黑洞的边界，在这个边界内，引力变得如此强大，以至于光都无法从其中逃离，这也使得黑洞本身无法直接被我们观测到，只能通过其对周围物质和时空的影响来间接推断它的存在 。

正是由于黑洞对时空的严重扭曲，导致了其附近出现了显著的时间膨胀效应 。

在广义相对论中，引力越强的地方，时间流逝速度就越慢 。在黑洞附近，强大的引力使得时间的流逝速度与远离黑洞的区域相比，发生了极大的变化 。这就意味着，在黑洞附近度过的极短时间，在远离黑洞的地球上可能已经过去了漫长的岁月 。

例如，在某些极端情况下，在黑洞附近 1 小时，就可能相当于地球 7 年 。这种巨大的时间差异，正是时空扭曲所带来的神奇而又令人难以理解的结果 。

在科幻电影《星际穿越》中，米勒行星的设定为我们生动地展示了黑洞附近时间膨胀的奇妙景象 。米勒行星是一颗围绕着超大质量黑洞 “卡冈图雅” 公转的行星，它所处的位置极为特殊，几乎快要被黑洞的引力拽进去 。

这颗行星的轨道半径只有 1.06 天文单位，与日地距离相当 。由于受到黑洞强大引力的影响，米勒行星的轨道速度达到了光速的 54.5%，轨道周期仅 1.7 小时 。同时，它还遭受着巨大的潮汐效应，从而产生了滔天巨浪，使其成为了一颗水行星 。

然而，电影情节虽然精彩，但背后的科学依据和可能存在的科学漏洞也值得我们探讨 。从科学依据来看，电影中关于时间膨胀的设定是基于广义相对论的引力时间膨胀效应，这是有坚实的科学理论基础的 。

许多科学家通过理论计算和天文观测，都证实了在强引力场中时间确实会变慢 。例如，通过对一些中子星和黑洞附近的观测，发现它们周围的物质运动和辐射现象都与广义相对论的预测相符 。此外，电影中对黑洞周围时空弯曲的视觉呈现，也是经过科学顾问的精心设计，尽可能地符合目前科学界对黑洞的认知 。

但是，电影中也存在一些可能的科学漏洞 。

在电影中，主角们的飞船直接靠近黑洞并穿越其周围的吸积盘，这在现实中几乎是不可能的 。黑洞的吸积盘是由被黑洞引力吸引并加速的物质组成，这些物质在高速运动中相互摩擦，会产生极高的温度和强烈的辐射 。

以人类目前对物理规律的理解，任何已知的物质都无法承受这样的高温和辐射，飞船在靠近吸积盘时就会被瞬间熔化蒸发 。此外，关于米勒行星的存在和稳定性也存在一些疑问 。在如此靠近黑洞的位置，黑洞的潮汐力非常强大，这种潮汐力可能会对行星的结构和轨道稳定性产生巨大的影响，甚至有可能导致行星被潮汐力撕裂 。

虽然电影中没有明确说明米勒行星是如何在这样的环境下保持稳定的，但从科学角度来看，这是一个需要进一步探讨的问题 。

人们之所以会因时间膨胀效应而产生永生的误解，主要源于对时间膨胀相对性的理解不足 。

在日常生活中，我们习惯了牛顿的绝对时空观，认为时间是绝对且均匀流逝的，不受其他因素的干扰 。而相对论中的时间膨胀效应打破了这种传统认知，让我们看到时间的流逝速度竟然会受到速度和引力的影响 。这种全新的时空观与我们的日常直觉产生了强烈的冲突，使得我们在理解时间膨胀效应时容易出现偏差 。

当我们看到在黑洞附近 1 小时相当于地球 7 年这样令人惊叹的时间膨胀现象时，很容易直观地认为，身处黑洞附近的人时间流逝速度变得极慢，他们的寿命相对于地球上的人来说被极大地延长了，甚至可以趋近于永生 。

这种想法的根源在于，我们没有充分认识到时间膨胀是一个相对的概念，它必须在两个不同的参照系之间进行比较才能体现出来 。在单一的参照系内部，时间仍然按照正常的方式流逝，人们并不会感受到时间膨胀带来的任何异常 。

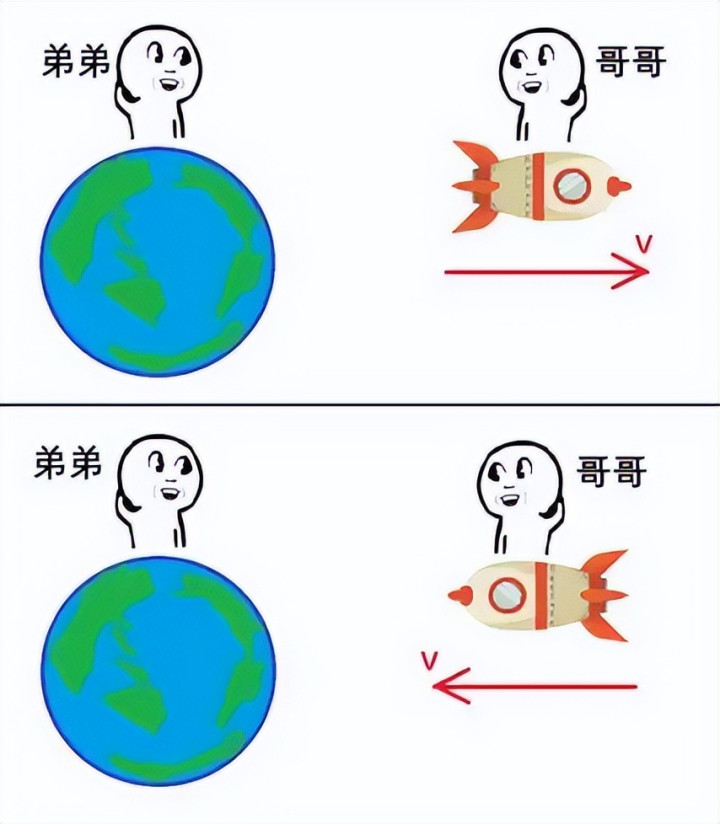
例如，假设有一对双胞胎，哥哥乘坐一艘接近光速的宇宙飞船进行星际旅行，弟弟则留在地球上 。在地球上的弟弟看来，哥哥的飞船速度极快，根据时间膨胀效应，哥哥飞船上的时间流逝速度会变得很慢 。当哥哥在飞船上度过了一年后返回地球，弟弟会发现自己已经度过了数十年，哥哥看起来比自己年轻了许多 。

然而，从哥哥的角度来看，他在飞船上的生活一切如常，他所经历的时间也是正常流逝的，他并不会觉得自己的寿命被延长了 。他在飞船上度过的一年，就像在地球上度过的一年一样，有着相同的生活节奏和生命体验 。这就是时间膨胀相对性的体现，不同参照系中的观察者对于时间流逝速度的感受是不同的，我们不能仅仅从一个参照系的角度去判断另一个参照系中的时间和寿命情况 。

时间膨胀效应仅仅是不同参照系之间的时间差异，它并不会改变个体自身的生命进程 。无论在何种参照系中，人体的生物学过程都是按照其自身的规律进行的 。

即使一个人处于时间膨胀效应显著的环境中，比如黑洞附近，他的细胞仍然会按照正常的生物学节奏进行分裂、衰老和死亡，他的身体也会经历正常的生长、发育、衰老和死亡过程 。他所感受到的时间流逝速度虽然在外界看来与其他参照系不同，但对于他自身而言，时间的体验和生命的进程并没有发生改变 。因此，从科学角度来看，时间膨胀效应并不能让人类实现永生 。